Фармакокинетика — различия между версиями
Febor (обсуждение | вклад) (→Фармакокинетика) |
Правкин (обсуждение | вклад) (→Двухкомпартментная модель) |
||
| (не показаны 2 промежуточные версии 2 участников) | |||
| Строка 5: | Строка 5: | ||
=== Однокомпартментная модель === | === Однокомпартментная модель === | ||
| − | + | [[Image:Ph_4_10.jpg|250px|thumb|right|Рис. 4.10 Схема открытой однокомпартментной фармакокинетической модели, предложенная для описания распределения лекарства. Концентрация лекарства в плазме (Ср) определяется скоростью его абсорбции (ка — константа скорости абсорбции), условным объемом распределения (Vd) и скоростью 30 элиминации лекарства (к). При парентеральном одномоментном введении лекарства абсорбция происходит мгновенно.]] | |
Согласно простейшей модели, организм рассматривается как единое однородное пространство (компартмент), в которое лекарство вводят и из которого оно элиминируется (рис. 4.10). Предполагается, что введенное лекарство сразу же распределяется по всему пространству. Если элиминация является кинетическим процессом первого порядка, то ее скорость пропорциональна концентрации в плазме, т.е. лекарство выводится экспоненциально. Математическое уравнение для этого экспоненциального соотношения выглядит так: | Согласно простейшей модели, организм рассматривается как единое однородное пространство (компартмент), в которое лекарство вводят и из которого оно элиминируется (рис. 4.10). Предполагается, что введенное лекарство сразу же распределяется по всему пространству. Если элиминация является кинетическим процессом первого порядка, то ее скорость пропорциональна концентрации в плазме, т.е. лекарство выводится экспоненциально. Математическое уравнение для этого экспоненциального соотношения выглядит так: | ||
| − | Ct = С0 • | + | Ct = С0 • e_k<sub>el</sub>t, (ф. 4.2) |
| − | |||
| − | |||
| + | где Ct — концентрация в плазме в данное время (t), С0 — вычисленная начальная концентрация в плазме при t = 0, kel — константа скорости элиминации, е — основание натурального логарифма. Если взять логарифм концентрации в плазме, экспоненциальный процесс выглядит в виде прямой линии (рис. 4.11). Наклон линии на рис. 4.11 в действительности составляет k<sub>el</sub>/2,303. Деление на 2,303 необходимо потому, что концентрация в плазме дана в десятичном логарифме, а не в логарифме с основанием е. Такое представление использовано на рис. 4.11, т.к. десятичное основание более знакомо фармакологам. Если начальную экстраполированную концентрацию лекарства (С0) в компартменте разделить на введенную дозу, получают теоретический объем, необходимый для описания дозы лекарства. Это пространство называют условным объемом распределения (Vd). | ||
| + | [[Image:Ph_4_11.jpg|250px|thumb|right|Рис. 4.11 Изменение концентрации лекарства в плазме в зависимости от времени после внутривенного введения: открытая однокомпартментная фармакокинетическая модель. Экстраполяция линии (ее наклон к) на время «ноль» позволяет определить инициальную концентрацию лекарства (С0) в компартменте при условии мгновенного распределения. Т1/2 — период полувыведения (в данном случае его значение равно 5)]] | ||
В то время как константа скорости элиминации показывает, как быстро элиминируется лекарство, расчет с использованием kel позволяет определить Т1/2, т.е. время, в течение которого концентрация лекарства в плазме падает на 50%. Поскольку падение концентрации лекарства со временем в логарифмическом исчислении является линейным, величина Т1/2 будет постоянной независимо от концентрации лекарства. Отношение kel и Т1/2 описывает уравнение: | В то время как константа скорости элиминации показывает, как быстро элиминируется лекарство, расчет с использованием kel позволяет определить Т1/2, т.е. время, в течение которого концентрация лекарства в плазме падает на 50%. Поскольку падение концентрации лекарства со временем в логарифмическом исчислении является линейным, величина Т1/2 будет постоянной независимо от концентрации лекарства. Отношение kel и Т1/2 описывает уравнение: | ||
| − | Т1/2 х | + | Т1/2 х k<sub>el</sub> = 0,693 (ф. 4.3) |
| − | |||
| − | |||
| − | + | Поскольку величина T1/2 связана с Vd, значение Т1/2 не всегда отражает способность организма элиминировать лекарство. Предпочитаемый кинетический термин, показывающий способность организма удалять лекарство из кровотока, — это клиренс плазмы (Clp), равный Vd X k<sub>el</sub>. Клиренс остается постоянным для большинства лекарств, если механизмы элиминации не изменяются под влиянием патологических процессов и/или физиологических факторов. | |
| − | + | [[Image:Ph_4_12.jpg|250px|thumb|right|Рис. 4.12 Изменение концентрации лекарства в плазме в зависимости от времени после перорального приема: открытая однокомпартментная фармакокинетическая модель. Форма кривой отличается от прямой линии на рис. 4.11. Т1/2 — период полувыведения.]] | |
| − | + | На рис. 4.11 показано снижение концентрации лекарства в плазме после его в/в введения. Однако при пероральном приеме необходимо время для абсорбции, и кривая снижения концентрации напоминает картину, изображенную на рис. 4.12. Форма кривой соотношения концентрации лекарства в плазме и времени отражает взаимодействие двух процессов первого порядка: поступления (абсорбции) вещества в одиночный кинетический компартмент и исчезновения (элиминации) вещества из него. Расчет Vd, Т1/2, k<sub>el</sub> и Сlр тот же самый, как после в/в введения, однако некоторые из производных параметров (Vd и Сlр) будут возрастать, если происходит значительная потеря лекарства до абсорбции (предсистемная элиминация вещества). Эта ситуация возникает в результате того, что концентрация вещества в плазме уменьшается вследствие предсистемной элиминация вещества, поэтому определение инициальной концентрации лекарства (С0) дает сниженную величину. Эта простая модель единственного однородного компартмента с кинетикой первого порядка вполне пригодна для расчета режима дозировки большинства лекарств. | |
| − | |||
| − | Рис. 4.12 Изменение концентрации лекарства в плазме в зависимости от времени после перорального приема: открытая однокомпартментная фармакокинетическая модель. Форма кривой отличается от прямой линии на рис. 4.11. | ||
| − | |||
| − | На рис. 4.11 показано снижение концентрации лекарства в плазме после его в/в введения. Однако при пероральном приеме необходимо время для абсорбции, и кривая снижения концентрации напоминает картину, изображенную на рис. 4.12. Форма кривой соотношения концентрации лекарства в плазме и времени отражает взаимодействие двух процессов первого порядка: поступления (абсорбции) вещества в одиночный кинетический компартмент и исчезновения (элиминации) вещества из него. Расчет Vd, Т1/2, | ||
=== Двухкомпартментная модель === | === Двухкомпартментная модель === | ||
| − | + | [[Image:Ph_4_13.jpg|250px|thumb|left|Рис. 4.13]] | |
| − | Для некоторых лекарств график, изображающий соотношение логарифма концентрации в плазме и времени, имеет криволинейную форму (рис. 4.13). Чтобы объяснить это явление, требуется расширить однокомпартментную модель. В простейшем виде организм следует рассматривать как двухкомпартментную модель (рис. 4.14). С определенным основанием можно считать, что объяснить криволинейный график на рис. 4.13 можно двумя линейными процессами. Эти два процесса известны под названием а- и β-фаз и характеризуются соответствующими для каждой из них константами скорости элиминации и Т1/2. Согласно этой модели, константа скорости кβ конечной линейной фазы (β) не та, что у | + | Для некоторых лекарств график, изображающий соотношение логарифма концентрации в плазме и времени, имеет криволинейную форму (рис. 4.13). Чтобы объяснить это явление, требуется расширить однокомпартментную модель. В простейшем виде организм следует рассматривать как двухкомпартментную модель (рис. 4.14). С определенным основанием можно считать, что объяснить криволинейный график на рис. 4.13 можно двумя линейными процессами. Эти два процесса известны под названием а- и β-фаз и характеризуются соответствующими для каждой из них константами скорости элиминации и Т1/2. Согласно этой модели, константа скорости кβ конечной линейной фазы (β) не та, что у k<sub>el</sub> на рис. 4.11 (модель одного компартмента). β-Фаза представляет собой более медленный процесс. Чем больше расхождение между кβ и k<sub>el</sub>, тем больше ошибка, если считать правомерной модель одного компартмента. К счастью, для большинства лекарств расхождение между кβ и k<sub>el</sub> не так велико, как межиндивидуальные различия кинетики, поэтому открытая модель одного компартмента служит приемлемой клинической аппроксимацией для индивидуального выбора дозировки. |
| − | + | [[Image:Ph_4_14.jpg|250px|thumb|left|Рис. 4.14]] | |
Очевидно, что как одно-, так и двухкомпартментные модели дают чрезмерно упрощенное представление о распределении лекарств в организме, где лекарственные вещества абсорбируются и удаляются посредством метаболизма и экскреции. Когда расхождения в модельном распределении лекарств становятся клинически очевидными для данного лекарства, его применение следует рассматривать как особый случай более сложного соотношения распределение-эффект. Лекарства, подвергаемые дозозависимому распределению (например, фенитоин, аспирин), относятся к этой специальной категории более сложного соотношения между дозой, концентрацией и фармакологическими эффектами. | Очевидно, что как одно-, так и двухкомпартментные модели дают чрезмерно упрощенное представление о распределении лекарств в организме, где лекарственные вещества абсорбируются и удаляются посредством метаболизма и экскреции. Когда расхождения в модельном распределении лекарств становятся клинически очевидными для данного лекарства, его применение следует рассматривать как особый случай более сложного соотношения распределение-эффект. Лекарства, подвергаемые дозозависимому распределению (например, фенитоин, аспирин), относятся к этой специальной категории более сложного соотношения между дозой, концентрацией и фармакологическими эффектами. | ||
| + | [[Image:Ph_4_15.jpg|250px|thumb|left|Рис. 4.15]] | ||
| + | ''Описание к Рис. 4.13'' Изменение концентрации лекарства в плазме в зависимости от времени после одномоментного внутривенного введения: открытая двухкомпартментная фармакокинетическая модель. Константа скорости конечной фазы III отличается от k<sub>el</sub>, и снижение концентрации со временем отражает более сложное соотношение между распределением и элиминацией лекарства. Начальное более быстрое падение концентрации циркулирующего лекарства (а) отражает в основном его перераспределение в периферический компартмент (Vp) (см. рис. 4.14) плюс незначительный компонент элиминации. Конечная, выраженная прямой линией фаза, отражающая зависимость концентрации в плазме от времени, представляет собой композит элиминации лекарства, замедленной возвратом вещества из Vp в центральный компартмент, в котором вещество распределяется быстро (Vc); тем самым снижается видимая скорость удаления лекарства из плазмы. Эту фазу обозначают как фазу кр. Обратная экстраполяция на время «ноль» дает отрезок, отсекаемый на координатной оси в точке В. Экстраполированное значение кр вычитают из наблюдаемой концентрации лекарства в то же самое время после его введения и откладывают на графике оставшуюся величину. Линия регрессии, проведенная через эти точки, дает наклон к„ и отрезок, отсекаемый на координатной оси в точке А, отражающий распределение лекарства в Vp. | ||
| − | Рис. 4. | + | ''Описание к Рис. 4.14'' Схема открытой двухкомпартментной фармакокинетической модели, отражающая концентрации лекарства после внутривенного введения. При одномоментном (болюсном) в/в введении величина к„ несущественна, и в модели ею можно пренебречь. Если лекарство вводят путем инфузии, ка представляет собой константу нулевого порядка, равную скорости инфузии вещества. Существует центральный компартмент, в котором лекарство распределяется быстро (Vc) и из которого оно элиминируется, и периферический компартмент, в котором лекарство может распределяться (Vp), а затем возвращаться, выравнивая изменения концентрации вещества в центральном компартменте, когда лекарство элиминируется. k<sub>el</sub> — константа элиминации. |
| − | + | ''Описание к Рис. 4.15'' Уравнения фармакокинетического распределения лекарства в отсутствие компартментализации. Константа конечной скорости распределения здесь обозначена А,, и ее интерпретация отличается от таковой для двух моделей, представленных на рис. 4.10-4.14. Введен новый расчет, называемый площадью под кривой (ППК), соответствующей соотношению между концентрацией в плазме и временем. С1р — клиренс плазмы; Т1/2 — период полувыведения; Vd — условный объем распределения. | |
| − | |||
| − | Рис. 4.15 Уравнения фармакокинетического распределения лекарства в отсутствие компартментализации. Константа конечной скорости распределения здесь обозначена А,, и ее интерпретация отличается от таковой для двух моделей, представленных на рис. 4.10-4.14. Введен новый расчет, называемый площадью под кривой (ППК), соответствующей соотношению между концентрацией в плазме и временем. С1р — клиренс плазмы; Т1/2 — период полувыведения; Vd — условный объем распределения. | ||
'''Продолжительность действия лекарств''' | '''Продолжительность действия лекарств''' | ||
| Строка 53: | Строка 47: | ||
Большинство лекарств применяют длительно. Для лекарств с элиминацией первого порядка общее количество вещества в организме возрастает, пока экскретируемое количество не становится равным введенной дозе в расчете на единицу времени, т.е. концентрация в плазме достигает стационарного состояния. Время достижения этого состояния для таких лекарств зависит только от конечного Т1/2. Расчет показывает, что 94 и 97% стационарного состояния создаются через 4 и 5 Т1/2 соответственно. Для практических целей принимают, что стационарное состояние в это время существует (рис. 4.16). Чем чаще вводят дозу лекарства, тем выше его количество в организме при стационарном состоянии и тем меньше вариация между концентрацией в плазме на пике и минимальной концентрацией. Чем реже вводят лекарство, тем ниже его количество в организме при стационарном состоянии и тем больше различие между концентрацией в плазме на пике и минимальной концентрацией. Если интервал между введениями больше, чем 2 Т1/2, накопление лекарства при длительном приеме внутрь считается клинически несущественным. | Большинство лекарств применяют длительно. Для лекарств с элиминацией первого порядка общее количество вещества в организме возрастает, пока экскретируемое количество не становится равным введенной дозе в расчете на единицу времени, т.е. концентрация в плазме достигает стационарного состояния. Время достижения этого состояния для таких лекарств зависит только от конечного Т1/2. Расчет показывает, что 94 и 97% стационарного состояния создаются через 4 и 5 Т1/2 соответственно. Для практических целей принимают, что стационарное состояние в это время существует (рис. 4.16). Чем чаще вводят дозу лекарства, тем выше его количество в организме при стационарном состоянии и тем меньше вариация между концентрацией в плазме на пике и минимальной концентрацией. Чем реже вводят лекарство, тем ниже его количество в организме при стационарном состоянии и тем больше различие между концентрацией в плазме на пике и минимальной концентрацией. Если интервал между введениями больше, чем 2 Т1/2, накопление лекарства при длительном приеме внутрь считается клинически несущественным. | ||
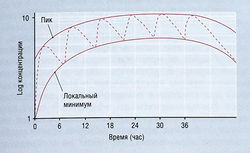
| − | + | [[Image:Ph_4_16.jpg|250px|thumb|right|Рис. 4.16 График, отображающий соотношение между концентрацией лекарства в плазме и временем после [[Пероральный путь введения лекарств|перорального приема]] 6 доз лекарства каждые 6 час, когда конечный период полувыведения (Т1/2) составляет 6 час. Эффективное стационарное равновесное состояние возникает через 24-30 час (4-5 Т1/2) после начала приема лекарства.]] | |
'''Фармокинетика''' | '''Фармокинетика''' | ||
| Строка 67: | Строка 61: | ||
*Т1/2 лекарства в плазме не отражает метаболической способности, если изменяется условный объем распределения | *Т1/2 лекарства в плазме не отражает метаболической способности, если изменяется условный объем распределения | ||
| − | |||
| − | |||
'''Для быстрого создания терапевтической концентрации лекарства в плазме можно ввести ударную дозу (дозу насыщения)''' | '''Для быстрого создания терапевтической концентрации лекарства в плазме можно ввести ударную дозу (дозу насыщения)''' | ||
| Строка 79: | Строка 71: | ||
Поддерживающая доза (мг/кг) = Сlр (л/кг/час) X Css (мг/л) X t (час) (ф. 4.5) | Поддерживающая доза (мг/кг) = Сlр (л/кг/час) X Css (мг/л) X t (час) (ф. 4.5) | ||
| + | |||
| + | == Читайте также == | ||
| + | |||
| + | *[[Пути введения лекарственных средств]] | ||
| + | *[[Абсорбция]] | ||
| + | *[[Распределение лекарственных средств]] | ||
| + | *[[Метаболизм препаратов и лекарств]] | ||
| + | *[[Экскреция (выведение) лекарственных средств]] | ||
| + | *[[Нелинейная фармакокинетика]] | ||
| + | *[[Влияние пола, возраста, наследственности на действие лекарственных средств]] | ||
| + | *[[Взаимодействие лекарственных средств]] | ||
| + | *[[Влияние заболеваний на действие лекарства]] | ||
Текущая версия на 11:12, 18 октября 2014
Категория:
«Фармакология».
Содержание
Фармакокинетика[править | править код]
Предметом фармакокинетики является анализ всех факторов, определяющих абсорбцию, распределение, метаболизм и экскрецию лекарственных веществ. Термин отражает скорость перемещения (кинетика) лекарств (фармако) в организме и вне его.
Однокомпартментная модель[править | править код]
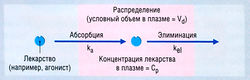
Согласно простейшей модели, организм рассматривается как единое однородное пространство (компартмент), в которое лекарство вводят и из которого оно элиминируется (рис. 4.10). Предполагается, что введенное лекарство сразу же распределяется по всему пространству. Если элиминация является кинетическим процессом первого порядка, то ее скорость пропорциональна концентрации в плазме, т.е. лекарство выводится экспоненциально. Математическое уравнение для этого экспоненциального соотношения выглядит так:
Ct = С0 • e_kelt, (ф. 4.2)
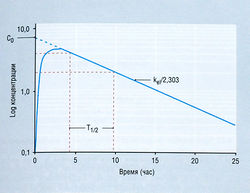
где Ct — концентрация в плазме в данное время (t), С0 — вычисленная начальная концентрация в плазме при t = 0, kel — константа скорости элиминации, е — основание натурального логарифма. Если взять логарифм концентрации в плазме, экспоненциальный процесс выглядит в виде прямой линии (рис. 4.11). Наклон линии на рис. 4.11 в действительности составляет kel/2,303. Деление на 2,303 необходимо потому, что концентрация в плазме дана в десятичном логарифме, а не в логарифме с основанием е. Такое представление использовано на рис. 4.11, т.к. десятичное основание более знакомо фармакологам. Если начальную экстраполированную концентрацию лекарства (С0) в компартменте разделить на введенную дозу, получают теоретический объем, необходимый для описания дозы лекарства. Это пространство называют условным объемом распределения (Vd).
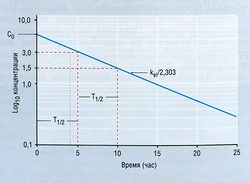
В то время как константа скорости элиминации показывает, как быстро элиминируется лекарство, расчет с использованием kel позволяет определить Т1/2, т.е. время, в течение которого концентрация лекарства в плазме падает на 50%. Поскольку падение концентрации лекарства со временем в логарифмическом исчислении является линейным, величина Т1/2 будет постоянной независимо от концентрации лекарства. Отношение kel и Т1/2 описывает уравнение:
Т1/2 х kel = 0,693 (ф. 4.3)
Поскольку величина T1/2 связана с Vd, значение Т1/2 не всегда отражает способность организма элиминировать лекарство. Предпочитаемый кинетический термин, показывающий способность организма удалять лекарство из кровотока, — это клиренс плазмы (Clp), равный Vd X kel. Клиренс остается постоянным для большинства лекарств, если механизмы элиминации не изменяются под влиянием патологических процессов и/или физиологических факторов.
На рис. 4.11 показано снижение концентрации лекарства в плазме после его в/в введения. Однако при пероральном приеме необходимо время для абсорбции, и кривая снижения концентрации напоминает картину, изображенную на рис. 4.12. Форма кривой соотношения концентрации лекарства в плазме и времени отражает взаимодействие двух процессов первого порядка: поступления (абсорбции) вещества в одиночный кинетический компартмент и исчезновения (элиминации) вещества из него. Расчет Vd, Т1/2, kel и Сlр тот же самый, как после в/в введения, однако некоторые из производных параметров (Vd и Сlр) будут возрастать, если происходит значительная потеря лекарства до абсорбции (предсистемная элиминация вещества). Эта ситуация возникает в результате того, что концентрация вещества в плазме уменьшается вследствие предсистемной элиминация вещества, поэтому определение инициальной концентрации лекарства (С0) дает сниженную величину. Эта простая модель единственного однородного компартмента с кинетикой первого порядка вполне пригодна для расчета режима дозировки большинства лекарств.
Двухкомпартментная модель[править | править код]
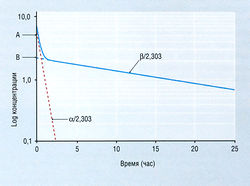
Для некоторых лекарств график, изображающий соотношение логарифма концентрации в плазме и времени, имеет криволинейную форму (рис. 4.13). Чтобы объяснить это явление, требуется расширить однокомпартментную модель. В простейшем виде организм следует рассматривать как двухкомпартментную модель (рис. 4.14). С определенным основанием можно считать, что объяснить криволинейный график на рис. 4.13 можно двумя линейными процессами. Эти два процесса известны под названием а- и β-фаз и характеризуются соответствующими для каждой из них константами скорости элиминации и Т1/2. Согласно этой модели, константа скорости кβ конечной линейной фазы (β) не та, что у kel на рис. 4.11 (модель одного компартмента). β-Фаза представляет собой более медленный процесс. Чем больше расхождение между кβ и kel, тем больше ошибка, если считать правомерной модель одного компартмента. К счастью, для большинства лекарств расхождение между кβ и kel не так велико, как межиндивидуальные различия кинетики, поэтому открытая модель одного компартмента служит приемлемой клинической аппроксимацией для индивидуального выбора дозировки.
Очевидно, что как одно-, так и двухкомпартментные модели дают чрезмерно упрощенное представление о распределении лекарств в организме, где лекарственные вещества абсорбируются и удаляются посредством метаболизма и экскреции. Когда расхождения в модельном распределении лекарств становятся клинически очевидными для данного лекарства, его применение следует рассматривать как особый случай более сложного соотношения распределение-эффект. Лекарства, подвергаемые дозозависимому распределению (например, фенитоин, аспирин), относятся к этой специальной категории более сложного соотношения между дозой, концентрацией и фармакологическими эффектами.
Описание к Рис. 4.13 Изменение концентрации лекарства в плазме в зависимости от времени после одномоментного внутривенного введения: открытая двухкомпартментная фармакокинетическая модель. Константа скорости конечной фазы III отличается от kel, и снижение концентрации со временем отражает более сложное соотношение между распределением и элиминацией лекарства. Начальное более быстрое падение концентрации циркулирующего лекарства (а) отражает в основном его перераспределение в периферический компартмент (Vp) (см. рис. 4.14) плюс незначительный компонент элиминации. Конечная, выраженная прямой линией фаза, отражающая зависимость концентрации в плазме от времени, представляет собой композит элиминации лекарства, замедленной возвратом вещества из Vp в центральный компартмент, в котором вещество распределяется быстро (Vc); тем самым снижается видимая скорость удаления лекарства из плазмы. Эту фазу обозначают как фазу кр. Обратная экстраполяция на время «ноль» дает отрезок, отсекаемый на координатной оси в точке В. Экстраполированное значение кр вычитают из наблюдаемой концентрации лекарства в то же самое время после его введения и откладывают на графике оставшуюся величину. Линия регрессии, проведенная через эти точки, дает наклон к„ и отрезок, отсекаемый на координатной оси в точке А, отражающий распределение лекарства в Vp.
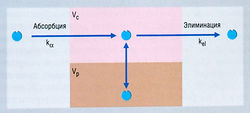
Описание к Рис. 4.14 Схема открытой двухкомпартментной фармакокинетической модели, отражающая концентрации лекарства после внутривенного введения. При одномоментном (болюсном) в/в введении величина к„ несущественна, и в модели ею можно пренебречь. Если лекарство вводят путем инфузии, ка представляет собой константу нулевого порядка, равную скорости инфузии вещества. Существует центральный компартмент, в котором лекарство распределяется быстро (Vc) и из которого оно элиминируется, и периферический компартмент, в котором лекарство может распределяться (Vp), а затем возвращаться, выравнивая изменения концентрации вещества в центральном компартменте, когда лекарство элиминируется. kel — константа элиминации.
Описание к Рис. 4.15 Уравнения фармакокинетического распределения лекарства в отсутствие компартментализации. Константа конечной скорости распределения здесь обозначена А,, и ее интерпретация отличается от таковой для двух моделей, представленных на рис. 4.10-4.14. Введен новый расчет, называемый площадью под кривой (ППК), соответствующей соотношению между концентрацией в плазме и временем. С1р — клиренс плазмы; Т1/2 — период полувыведения; Vd — условный объем распределения.
Продолжительность действия лекарств
- Клинически более важно знать действие лекарства во времени, а не фармакокинетику его концентрации. Между действием лекарства (эффекторная концентрация) и концентрацией в крови может существовать (а может и не быть) линейное или простое соотношение
- Время, необходимое для проявления эффектов лекарства, может быть гораздо длительнее, чем действия лекарства на его молекулярную мишень, т.к. система реагирования имеет собственные временные ограничения
- Например, β-блокаторы очень быстро замедляют частоту сердечных сокращений, тогда как для проявления антикоагулирующего действия варфарина требуется несколько дней
Подход без использования компартментного принципа[править | править код]
Этот подход используют для упрощенного определения фармакокинетических параметров, на основании которых можно рассчитать дозу лекарства. Многое в этом подходе заимствовано из открытой однокомпартментной модели. Площадь под кривой (ППК) концентрации представляет в интегральном виде соотношение между концентрацией в плазме и временем, и расчет кинетических параметров проводят соответственно уравнениям, приведенным на рис. 4.15. Этот метод до некоторой степени компенсирует экстраполяцию концентрации лекарства на С0 в модели одного компартмента, когда лекарство еще не абсорбировалось в организме после перорального приема.
Расчет дозировки[править | править код]
Большинство лекарств применяют длительно. Для лекарств с элиминацией первого порядка общее количество вещества в организме возрастает, пока экскретируемое количество не становится равным введенной дозе в расчете на единицу времени, т.е. концентрация в плазме достигает стационарного состояния. Время достижения этого состояния для таких лекарств зависит только от конечного Т1/2. Расчет показывает, что 94 и 97% стационарного состояния создаются через 4 и 5 Т1/2 соответственно. Для практических целей принимают, что стационарное состояние в это время существует (рис. 4.16). Чем чаще вводят дозу лекарства, тем выше его количество в организме при стационарном состоянии и тем меньше вариация между концентрацией в плазме на пике и минимальной концентрацией. Чем реже вводят лекарство, тем ниже его количество в организме при стационарном состоянии и тем больше различие между концентрацией в плазме на пике и минимальной концентрацией. Если интервал между введениями больше, чем 2 Т1/2, накопление лекарства при длительном приеме внутрь считается клинически несущественным.
Фармокинетика
- Большинство лекарств элиминируется из организма как постоянная фракция их концентрации в плазме (процесс первого порядка)
- Время достижения стационарного состояния зависит только от скорости элиминации лекарства
- Повторное введение лекарства приводит к его существенному накоплению, если его принимают внутрь с интервалами, меньшими чем двойной конечный период полувыведения (2 Т1/2)
- Практически время установления стационарного состояния составляет 4-5 Т1/2
- Количество лекарства в организме при стационарном состоянии зависит от частоты приема и величины дозы
- Т1/2 лекарства в плазме не отражает метаболической способности, если изменяется условный объем распределения
Для быстрого создания терапевтической концентрации лекарства в плазме можно ввести ударную дозу (дозу насыщения)
Ударную дозу лекарства рассчитывают на основании его Vd и желаемой концентрации в плазме при стационарном состоянии (Css):
Ударная доза (мг/кг) = = Vd (л/кг) X Css (мг/л) (ф. 4.4)
При в/в введении ударную дозу обычно инфузируют в течение короткого периода времени, чтобы снизить риск возникновения побочных эффектов, связанных с очень высокой концентрацией лекарства в кровотоке. Затем рассчитывают величину поддерживающей дозы, основываясь на Сlр и величине интервалов между дозами (t):
Поддерживающая доза (мг/кг) = Сlр (л/кг/час) X Css (мг/л) X t (час) (ф. 4.5)
Читайте также[править | править код]
- Пути введения лекарственных средств
- Абсорбция
- Распределение лекарственных средств
- Метаболизм препаратов и лекарств
- Экскреция (выведение) лекарственных средств
- Нелинейная фармакокинетика
- Влияние пола, возраста, наследственности на действие лекарственных средств
- Взаимодействие лекарственных средств
- Влияние заболеваний на действие лекарства